看到一篇非常不错的 Shader 入门文章，今天翻译并整理分享给大家。 今天，我们通过一个实际案例，完整实现一个流动渐变的着色器视觉效果。这个案例由 WebGL 着色器（Shader）驱动，核心原理是结合噪声函数和数学表达式，让色彩自然地流动变化。
这个案例非常适合作为 Shader 入门案例、涵盖了插值、颜色映射、渐变噪声等多个核心知识点。通过亲手实现它，你将对着色器编程建立起清晰的理解。
先看下最终效果：
颜色作为位置函数
构建渐变效果将归结为编写一个函数，该函数接收像素位置并返回一个颜色值：
type Position = { x: number, y: number };
function pixelColor({ x, y }: Position): Color;对于画布上的每个像素，我们将使用该像素的位置调用颜色函数来计算其颜色。一个画布帧可能渲染如下：
for (let x = 0; x < canvas.width; x++) {
for (let y = 0; y < canvas.height; y++) {
const color = pixelColor({ x, y });
canvas.drawPixel({ x, y }, color);
}
}首先，让我们编写一个生成线性渐变色的函数，如下所示：
为了生成这种红到蓝的渐变色，我们将用随画布宽度从 0 增加到 1 的混合因子来混合红色和蓝色——我们称这个混合因子为 。我们可以这样计算它：
function pixelColor({ x, y }: Position): Color {
const t = x / (canvas.width - 1);
}计算出混合因子 后，我们将用它来混合红色和蓝色：
const red = color("#ff0000");
const blue = color("#0000ff");
function pixelColor({ x, y }: Position): Color {
const t = x / (canvas.width - 1);
return mix(red, blue, t);
}mix 函数是一个插值函数，它使用介于 和 之间的混合因子（在我们的例子中是 ）在线性插值两个输入颜色之间。
一个用于两个数字的函数可以这样实现：
function mix(a: number, b: number, t: number) {
return a * (1 - t) + b * t;
}混合函数通常被称为“lerp”——线性插值的缩写。
一个用于两个颜色的函数工作方式相同，只是我们混合颜色分量。例如，混合两种 RGB 颜色时，我们会混合红、绿和蓝通道。
function mix(a: Color, b: Color, t: number) {
return new Color(
a.r * (1 - t) + b.r * t,
a.g * (1 - t) + b.g * t,
a.b * (1 - t) + b.b * t,
);
}无论如何， mix(red, blue, t) 在画布宽度（轴）上产生一个从红到蓝的渐变：
当 x ==0 时我们得到一个值为 ，给我们 100% 的红色。当 x == canvas.width -1 时我们得到一个值为 ，给我们 100% 的蓝色。如果我们得到 70% 的红色和 30% 的蓝色。
如果我们想要一个振荡渐变（从红色到蓝色再到红色，重复），我们可以通过使用 sin(x) 来计算混合因子来实现：
function pixelColor({ x, y }: Position): Color {
let t = sin(x);
t = (t + 1) / 2; // Normalize
return mix(red, blue, t);
}注意：sin 返回的是介于 -1 到 1 之间的值，而 mix 函数接受的是介于 0 到 1 之间的值。因此，我们通过将区间 [-1, 1] 重新映射到 [0, 1]，即使用公式 (t + 1) / 2，对 t 进行了归一化。
这产生了以下效果：
那些波浪非常细！这是因为我们在每个像素之间在红色和蓝色之间振荡。
我们可以通过定义一个频率倍数来控制振荡速率。它将决定渐变从红色振荡到蓝色再回到红色的像素数量。为了产生像素的波长，我们将频率倍数设置为：
const L = 40;
const frequency = (2 * PI) / L;
function pixelColor({ x, y }: Position): Color {
let t = sin(x * frequency);
// ...
}这会产生具有所需波长的振荡渐变——尝试使用滑块更改值来查看效果：
添加运动
到目前为止，我们只生成了静态图像。为了引入运动效果，我们将更新我们的颜色函数，使其接受一个 time 值。
function pixelColor({ x, y }: Position, time: number): Color;我们将 time 定义为经过的时间，以秒为单位。
通过将 time 加到像素的位置上，我们模拟了画布每秒向右滚动一个像素的效果：
let t = sin((x + time) * frequency);但是每秒滚动一个像素非常慢。让我们添加一个速度常量来控制滚动速度，并将 time 乘以它：
const S = 20;
let t = sin((x + time * S) * frequency);
这两个输入——时间和像素的位置——将成为驱动我们最终效果的主要组成部分。
我们将在本文的其余部分编写一个颜色函数，该函数将为每个像素计算颜色——以像素的位置和时间作为函数的输入。每个像素的颜色共同构成动画的一帧。
但请考虑需要完成的工作量。一个画布，就像上面的一样，包含像素。这意味着每帧都需要调用我们的像素函数——这对 CPU 来说每秒要执行 60 次，工作量巨大！这就是 WebGL 发挥作用的地方。
WebGL 着色器在 GPU 上运行，这对我们来说很有用，因为 GPU 是为高度并行计算而设计的。GPU 可以并行调用我们的颜色函数数千次，使得渲染单帧的任务变得轻而易举。
在概念上，没有变化。我们仍然要编写一个颜色函数，该函数接受一个位置和时间值，并返回一个颜色。但不再是使用 JavaScript 编写并在 CPU 上运行，而是使用 GLSL 编写并在 GPU 上运行。
WebGL 和 GLSL
WebGL 可以被视为 OpenGL 的一个子集，OpenGL 是一个跨平台的图形渲染 API。WebGL 基于 OpenGL ES——这是为嵌入式系统（如移动设备）设计的 OpenGL 规范。
这是一页列出了 OpenGL 和 WebGL 之间差异的页面。我们在这篇文章中不会遇到这些差异。
OpenGL 着色器是用 GLSL 编写的，GLSL 代表 OpenGL 着色语言。它是一种强类型语言，具有类似 C 的语法。
着色器有两种类型：顶点着色器和片元着色器，它们有不同的用途。我们的颜色函数将在片元着色器中运行（有时也称为“像素着色器”）。我们将在这里花费大部分时间。
设置 WebGL 渲染管线涉及大量的模板代码。我会尽量省略它，以便我们能专注于我们的主要目标，即创建一个酷炫的渐变效果。
在整个帖子中，我会链接到我找到的关于如何设置和操作 WebGL 的有用资源。
编写片元着色器
这是一个将每个像素设置为相同颜色的 WebGL 片元着色器。
void main() {
vec4 color = vec4(0.7, 0.1, 0.4, 1.0);
gl_FragColor = color;
}WebGL 片元着色器有一个 main 函数，它会对每个像素调用一次。 main 函数设置 gl_FragColor 的值——这是一个特殊变量，用于指定像素的颜色。
我们可以将 main 理解为颜色函数的入口点，将 gl_FragColor 理解为其返回值。
WebGL 颜色通过具有 3 或 4 个分量的向量表示： vec3 用于 RGB 颜色， vec4 用于 RGBA 颜色。前三个分量（RGB）分别是红色、绿色和蓝色分量。对于 4D 向量，第四个分量是颜色的 alpha 分量——即其不透明度。
vec3 red = vec3(1.0, 0.0, 0.0);
vec3 blue = vec3(0.0, 0.0, 1.0);
vec3 white = vec3(1.0, 1.0, 1.0);
vec4 semi_transparent_green = vec4(0.0, 1.0, 0.0, 0.5);WebGL 颜色使用分数表示法，其中每个分量是一个介于 0 和 1 之间的值。考虑着色器中的颜色：
void main() {
vec4 color = vec4(0.7, 0.1, 0.4, 1.0);
gl_FragColor = color;
}我们可以轻松地将分数 GLSL 颜色 vec3(0.7,0.1,0.4) 转换为基于百分比的 CSS 颜色 rgb(70%,10%,40%) 。我们还可以将分数乘以 255 以获得无符号整数表示 rgb(178,25,102) 。
无论如何，如果我们运行这个着色器，我们会看到每个像素都被设置为那种颜色：
让我们创建一个沿轴渐变到另一种颜色的线性渐变。让我们使用 rgb(229,154,25) — 它对应于 vec3(0.9,0.6,0.1) 中的 GLSL。
vec3 color_1 = vec3(0.7, 0.1, 0.4);
vec3 color_2 = vec3(0.9, 0.6, 0.1);要在轴上从 color_1 逐渐过渡到 color_2 ，我们需要当前像素的坐标。在 WebGL 片元着色器中，我们通过一个特殊的变量 gl_FragCoord 来获取这个坐标
float y = gl_FragCoord.y;float 对应一个 32 位浮点数。在这篇文章中，我们只会使用 float 和 int 这两种数值类型，它们都是 32 位的。
和之前一样，我们将使用像素的坐标通过除以画布高度来计算混合值。
const float CANVAS_WIDTH = 150.0;
float y = gl_FragCoord.y;
float t = y / (CANVAS_WIDTH - 1.0);注意：我已经配置了坐标，使得 gl_FragCoord 在左下角为 (0.0,0.0) ，在右上角为 (CANVAS_WIDTH -1, CANVAS_HEIGHT -1) 。这将在整篇文章中保持一致。
我们将使用 GLSL 的内置 mix 函数来混合这两种颜色。
vec3 color = mix(color_1, color_2, t);GLSL 有一系列内置的数学函数，例如 sin 、 clamp 和 pow 。
我们将新计算出的 color 赋值给 gl_FragColor ：
vec3 color = mix(color_1, color_2, t);
gl_FragColor = color;等等——我们遇到了编译时错误。
错误：‘assign’：不能从‘3 分量浮点向量’转换为‘FragColor 4 分量浮点向量’
这个错误有点晦涩，但它告诉我们我们不能将 vec3 color 赋值给 gl_FragColor ，因为 gl_FragColor 的类型是 vec4 。
换句话说，我们需要在将 color 传递给 gl_FragColor 之前为其添加一个 alpha 分量。我们可以这样做：
vec3 color = mix(color_1, color_2, t);
gl_FragColor = vec4(color, 1.0);这样就得到了一个线性渐变！
向量构造函数
你可能对上面的 vec4(color,1.0) 表达式感到疑惑——它等同于 vec4(vec3(...),1.0) ，这在 GLSL 中完全有效！
当将向量传递给向量构造函数时，输入向量的分量按从左到右的顺序读取——类似于 JavaScript 的展开语法。
vec3 a;
// this:
vec4 foo = vec4(a.x, a.y, a.z, 1.0);
// is equivalent to this:
vec4 foo = vec4(a, 1.0);你可以以任何你认为合适的方式组合数字和向量输入，只要传递给向量构造函数的值的总数是正确的：
vec4(1.0 vec2(2.0, 3.0), 4.0); // OK
vec4(vec2(1.0, 2.0), vec2(3.0, 4.0)); // OK
vec4(vec2(1.0, 2.0), 3.0); // Error, not enough components为不同区域上色
让我们将画布的下半部分涂成白色，如下所示：
要实现这一点，我们首先需要计算画布的中线位置：
const float MID_Y = CANVAS_HEIGHT * 0.5;然后我们可以通过减法来确定像素到这条线的有符号距离：
float y = gl_FragCoord.y;
float dist = MID_Y - y;决定我们的像素是否为白色，取决于它是否位于线下方，我们可以通过读取通过 sign 函数的距离符号来确定。 sign 函数返回该值是否为负数以及是否为正数。
float dist = MID_Y - y;
sign(dist); // -1.0 or 1.0我们可以通过将符号归一化到或通过计算得到一个 alpha（混合）值。
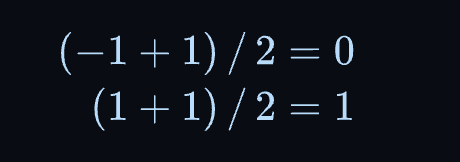
float alpha = (sign(dist) + 1.0) / 2.0;使用 alpha 种颜色混合 color 和 white ，将画布下半部分渲染为白色：
color = mix(color, white, alpha);
这里， alpha 代表我们的像素有多白。如果 alpha ==1.0 像素被着色为白色，但如果 alpha ==0.0 会保留 color 的原始值。
通过归一化符号并将结果传递给 mix 函数来计算 alpha 值，似乎有些过于绕弯。难道你不能直接使用 if 语句吗？
if (sign(dist) == 1.0) {
color = white;
}你可以这样做，但前提是你只想选择 100%的其中一种颜色。当我们扩展这个功能以在颜色之间平滑过渡时，使用条件语句将不再适用。
作为另一个要点，通常希望在 GPU 上运行的代码中避免分支（if-else 语句）。着色器代码中的分支代码比起无分支代码性能要差。
绘制任意曲线
我们目前将 MID_Y 下的所有内容都涂成白色，但线条不必由常数决定——我们可以使用任意表达式计算曲线的，并用它来计算 dist ：
float curve_y = <some expression>;
float dist = curve_y - y;这使得我们可以将任何曲线下的区域涂成白色。例如，我们可以将曲线定义为一个斜线
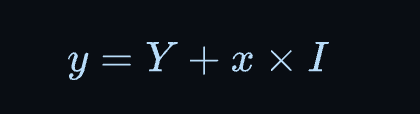
线的起始位置在哪里，是线的倾斜度。我们可以像这样将其放入代码中：
const float Y = 0.4 * CANVAS_HEIGHT;
const float I = 0.2;
float x = gl_FragCoord.x;
float curve_y = Y + x * I;这会在下面的画布中生成一条斜线——你可以调整以查看效果：
我们也可以像这样绘制一条抛物线：
// Adjust x=0 to be in the middle of the canvas
float x = gl_FragCoord.x - CANVAS_WIDTH / 2.0;
float curve_y = Y + pow(x, 2.0) / 40.0;
要点是我们可以根据需要定义曲线。
制作动画波浪
要绘制正弦波，我们可以将曲线定义为：
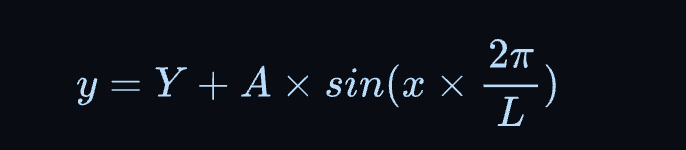
其中 是波浪的基线位置， 是波浪的振幅， 是波浪在像素中的长度。将其放入代码中，我们得到：
const float Y = 0.5 * CANVAS_HEIGHT;
const float A = 15.0;
const float L = 75.0;
const float frequency = (2.0 * PI) / L;
float curve_y = Y + sin(x * frequency) * A;这绘制了一个正弦波：
目前，一切都完全是静态的。为了让我们的着色器产生任何运动，我们需要引入一个时间变量。我们可以通过 uniforms 来实现这一点。
uniform float u_time;你可以将 uniforms 视为每绘制调用时的常量——全局变量，着色器只能读取这些变量。uniforms 的实际值由 JavaScript 端控制。
在给定的绘制调用中，每个着色器调用都将具有设置为相同值的统一变量。这就是“统一”这个名字的含义——在给定的绘制调用中，统一变量的值是一致的。然而，JavaScript 端可以在绘制调用之间更改统一变量的值。
统一变量在绘制调用中是常量，但它们不是编译时常量，这意味着你不能在 const 变量中使用统一变量的值。
统一变量可以是多种类型，例如浮点数、向量以及纹理（我们稍后会讨论纹理）。但 u_ 前缀是怎么回事？
uniform float u_time;给统一变量名加上 u_ 前缀是 GLSL 的惯例。如果你不这样做，也不会遇到编译错误，但给统一变量名加上 u_ 前缀是一个非常成熟的模式。
注意：对于属性名和 varying 名的命名也有类似的惯例（它们分别用 a_ 和 v_ 前缀），但我们在这篇文章中不会使用属性或 varying。
无论如何，现在 u_time 在我们的着色器中可用，我们可以开始产生运动。作为提醒，我们目前计算曲线值的方式如下：
float curve_y = Y + sin(x * W) * A;给像素位置加上 u_time 会随时间将波浪向左移动：
float curve_y = Y + sin((x + u_time) * W) * A;但每秒移动一个像素速度相当慢（ u_time 以秒为单位），所以我们将添加一个速度常数来控制速度：
const float S = 25.0;
float curve_y = Y + sin((x + u_time * S) * W) * A;尝试改变以看到速度变化：
将渐变应用于下半部分
与其下半部分是纯白色，不如我们把它做成渐变色（像上半部分一样）。
目前上半部分的渐变色由两种颜色组成： color_1 和 color_2 。让我们将它们重命名为 upper_color_1 和 upper_color_2 ：
vec3 upper_color_1 = vec3(0.7, 0.1, 0.4);
vec3 upper_color_2 = vec3(0.9, 0.6, 0.1);对于下半部分的渐变色，我们将引入两种新颜色： lower_color_1 和 lower_color_2 。
vec3 lower_color_1 = vec3(1.0, 0.7, 0.5);
vec3 lower_color_2 = vec3(1.0, 1.0, 0.9);我们将使用像素的位置计算一个值，用这个值沿着轴逐渐混合颜色：
float t = y / (CANVAS_HEIGHT - 1.0);
vec3 upper_color = mix(upper_color_1, upper_color_2, t);
vec3 lower_color = mix(lower_color_1, lower_color_2, t);通过这种方式，我们有效地计算出了两个渐变。然后我们将使用 alpha 来确定当前像素的颜色应该使用哪个渐变：
float alpha = (sign(curve_y - y) + 1.0) / 2.0;
vec3 color = mix(upper_color, lower_color, alpha);这会将渐变应用于两半：
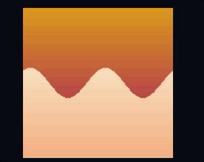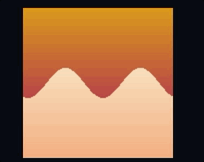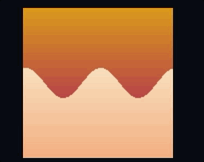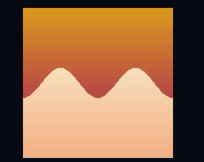
由于 alpha 的值是通过距离的符号计算得出的，因此它的值在波浪边缘会突然从变为 — 这就是产生锐利分割的原因。
让我们看看如何使用模糊效果使分割更平滑。
添加模糊效果
模糊效果并不是均匀地应用于波浪上——不同部分的波浪会应用不同量的模糊，并且这个量会随时间变化。
我们该如何实现这种效果？
高斯模糊
当思考如何解决模糊问题时，我首先想到的是使用高斯模糊。我打算通过噪声函数来确定应用模糊的程度，然后根据模糊量对相邻像素进行采样。
这是一个有效的方法——WebGL 中的渐进式模糊是可行的——但为了获得良好的模糊效果，我们需要采样大量相邻像素，而需要采样的像素数量会随着模糊半径的增大而不断增加。最终效果需要非常大的模糊半径，因此成本会非常快地变得非常高昂。
此外，为了能够以合理的性能采样相邻像素的 alpha 值，我们需要提前计算它们的 alpha 值。为此，我们需要将 alpha 通道预渲染到纹理中供我们采样，这需要设置另一个着色器和渲染通道。这不是什么大问题，但它会增加复杂性。
我选择了一种不需要采样邻近像素的方法。让我们看看。
使用有符号距离计算模糊效果
这是我们目前计算 alpha 的方式：
float dist = curve_y - y;
float alpha = (sign(dist) + 1.0) / 2.0;通过取距离的符号，我们总是得到 0%或 100%的不透明度——要么完全透明，要么完全不透明。让我们改为让 alpha 在多个像素上逐渐过渡。让我们为这个效果定义一个常量：
const float BLUR_AMOUNT = 50.0;我们将 alpha 的计算改为仅 dist / BLUR_AMOUNT 。
float alpha = dist / BLUR_AMOUNT;当 dist ==0.0 时，alpha 值为 ，而随着 dist 接近 BLUR_AMOUNT ，alpha 值接近 。这将导致 alpha 在所需像素数内从 变化到 ，但我们需要考虑的是
- 当
dist超过BLUR_AMOUNT时，alpha 会超过，并且 - 当
dist为负数时，alpha 会变成负数。
这两种情况都会导致问题（alpha 值应该只在 范围内），因此我们将使用内置的 clamp 函数将 alpha 限制在范围内：
float alpha = dist / BLUR_AMOUNT;
alpha = clamp(alpha, 0.0, 1.0);这会产生模糊效果，但我们可以观察到随着模糊程度的增加，波浪会“向下移动”——尝试使用滑块调整模糊程度：
我们可以通过将 alpha 从以下位置开始来修复下移问题：
float alpha = 0.5 + dist / BLUR_AMOUNT;
alpha = clamp(alpha, 0.0, 1.0);从该位置开始，当 dist 从 -BLUR_AMOUNT /2 变化到 BLUR_AMOUNT /2 时， alpha 会从 变化到 ，这使波浪保持居中：
现在让我们让模糊效果从左到右逐渐增强。为了逐渐增强模糊效果，我们可以沿着轴向线性插值，从无模糊到 BLUR_AMOUNT ，如下所示：
float t = gl_FragCoord.x / (CANVAS_WIDTH - 1)
float blur_amount = mix(1.0, BLUR_AMOUNT, t);使用 blur_amount 来计算 alpha，我们得到逐渐增强的模糊效果：
float alpha = dist / blur_amount;
alpha = clamp(alpha, 0.0, 1.0);
这构成了我们最终效果中模糊的基础。
当前的模糊效果看起来有点“原始”，但让我们暂时将其搁置。我们将在本文稍后将其做得非常棒。
现在让我们来制作一个看起来自然的波浪。
堆叠正弦波
我需要简单而自然的波浪状噪声函数时，经常使用堆叠的正弦波。这里是一个使用堆叠正弦波创建的波浪示例：
想法是将多个具有不同波长、振幅和相速度的正弦波的输出相加。
取以下纯正弦波：
如果你将它们组合成一个单一波浪，你会得到一个有趣的最终波浪：
单个正弦波的方程是
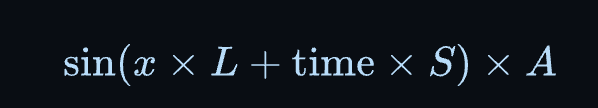
其中，x、A 和ω是控制波浪不同方面的变量：
- L 决定了波长，
- S 决定了相位演化速度，和
- A 决定波浪的振幅。
最终的波浪可以描述为这些波浪的总和：
将其写成代码，看起来是这样的：
float sum = 0.0;
sum += sin(x * L1 + u_time * S1) * A1;
sum += sin(x * L2 + u_time * S2) * A2;
sum += sin(x * L3 + u_time * S3) * A3;
...
return sum;那么问题就在于找到每个正弦波的值，当它们堆叠在一起时，能产生一个看起来很漂亮的最终波形。
在寻找这些值时，我首先创建了一个“基线波形”，将、的分量设置为感觉合适的值。我选择了这些值：
const float L = 0.015;
const float S = 0.6;
const float A = 32.0;
float sum = sin(x * L + u_time * S) * A;它们产生了以下波形：
这个波形大致是我想要的最终波形形状，因此这些值作为很好的基线。
我接着添加更多使用基线值、乘以一些常数的正弦波。经过一些反复试验，最终得到了以下结果：
float sum = 0.0;
sum += sin(x * (L / 1.000) + u_time * 0.90 * S) * A * 0.64;
sum += sin(x * (L / 1.153) + u_time * 1.15 * S) * A * 0.40;
sum += sin(x * (L / 1.622) + u_time * -0.75 * S) * A * 0.48;
sum += sin(x * (L / 1.871) + u_time * 0.65 * S) * A * 0.43;
sum += sin(x * (L / 2.013) + u_time * -1.05 * S) * A * 0.32;观察第 3 和第 5 个波浪是如何乘以一个负数的。让部分波浪向相反方向运动，可以防止最终的波浪给人一种以恒定速率向一个方向运动的错觉。
这五个正弦波给我们提供了一个相当自然的最终波形：
由于所有正弦波都由 、 、 定义，我们可以通过调整这些常数来一起调节波形。增加 使波形更快，增加 使波形更短，增加 使波形更高。尝试改变 和 的值：
我们实际上不会在我们的最终效果中使用堆叠的正弦波。然而，我们将使用堆叠不同尺度和速度波形的想法。
Simplex noise
简单的噪声是由 Ken Perlin 开发的一族-d 维梯度噪声函数。Ken 于 1983 年首次引入了“经典”Perlin 噪声，并于 2001 年创建了简单的噪声，以解决 Perlin 噪声的一些缺点。
一个简单的噪声函数的维度指的是该函数需要多少个数值输入（2D 简单的噪声函数需要两个数值参数，3D 函数需要三个）。所有简单的噪声函数返回一个介于和之间的单个数值。
2D 简单的噪声经常被使用，例如，在电子游戏中程序生成地形。这是一个使用 2D 简单的噪声创建的纹理示例，可以用作高度图：
它是通过使用 2D 简单的噪声函数的输出，并将像素的坐标和作为输入来计算每个像素的亮度生成的。
const float L = 0.02;
float x = gl_FragCoord.x * L;
float y = gl_FragCoord.y * L;
float lightness = (simplex_noise(x, y) + 1.0) / 2.0;
gl_FragColor = vec4(vec3(lightness), 1.0);注意：我使用的 simplex_noise 实现可以在这个 GitHub 仓库中找到。
L 控制坐标的缩放。随着增加，噪声会变得更小。
我们将使用 2D 简单噪声来创建一个动画化的 1D 波。这个想法可能不太明显，所以让我们看看它是如何工作的。
使用 2D 噪声的 1D 动画
考虑以下几点：
这些点在 x 轴和 y 轴上排列成网格配置，每个点的坐标通过 simplex_noise(x, z) 计算得出：
for (const point of points) {
const { x, z } = point;
point.y = simplex_noise(x, z);
}通过这种方式，我们有效地将 2D 输入（x 轴和 y 轴坐标）创建成了 3D 表面。
足够了，但这如何与生成动画波浪相关？
考虑如果我们使用时间作为坐标会发生什么。随着时间流逝，的值增加，从而给我们沿轴的表面不同 1D 切片。这里有一个可视化：
将这应用于我们的 2D 画布代码相当简单：
uniform float u_time;
const float L = 0.0015;
const float S = 0.12;
const float A = 40.0;
float x = gl_FragCoord.x;
float curve_y = MID_Y + simplex_noise(x * L, u_time * S) * A;这给我们带来一个平滑的动画波浪：
一个简单的单形噪声函数调用就能产生非常自然的水波效果！
同样的三个变量 ，决定了我们水波的特征。我们通过缩放 来使水波在水平轴上变短或变长：
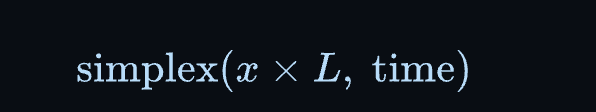我们通过缩放 来控制水波的发展速度——即我们在上方可视化中沿轴移动的速度：
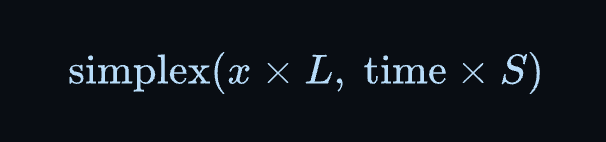最后，我们通过缩放函数的输出值来控制水波的振幅（高度）。
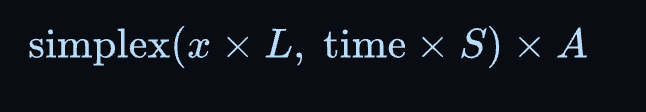Simplex 噪声返回一个介于-1 和 1 之间的值，因此要生成一个高度为 1 的波浪，你需要将频率设置为 1。
尽管 Simplex 波浪看起来很自然，但我发现其波峰和波谷看起来过于均匀和可预测。
这就是堆叠的作用所在。我们可以堆叠不同长度和速度的 Simplex 波浪，以获得一个更有趣的最终波浪。我调整了常数并添加了一些逐渐增大的波浪——有些较慢，有些较快。这是我最终得到的效果：
const float L = 0.0018;
const float S = 0.04;
const float A = 40.0;
float noise = 0.0;
noise += simplex_noise(x * (L / 1.00), u_time * S * 1.00)) * A * 0.85;
noise += simplex_noise(x * (L / 1.30), u_time * S * 1.26)) * A * 1.15;
noise += simplex_noise(x * (L / 1.86), u_time * S * 1.09)) * A * 0.60;
noise += simplex_noise(x * (L / 3.25), u_time * S * 0.89)) * A * 0.40;这产生了一个既自然又视觉上有趣的波浪。
看起来很棒，但我感觉缺少一个组件，那就是方向流动。波浪太“静止”，让它显得有些不自然。
要让波浪向左流动，我们可以在 x 组件中添加 u_time ，并通过一个常数来调整流动的量。
const float F = 0.043;
float noise = 0.0;
noise += simplex_noise(x * (L / 1.00) + F * u_time, ...) * ...;
noise += simplex_noise(x * (L / 1.30) + F * u_time, ...) * ...;
noise += simplex_noise(x * (L / 1.86) + F * u_time, ...) * ...;
noise += simplex_noise(x * (L / 3.25) + F * u_time, ...) * ...;这给波浪增加了一种微妙的流动感。尝试改变流动的量，感受它带来的不同：
流动的量可能感觉微妙，但这正是有意为之。如果流动很容易被注意到，那就太多了。
我认为我们有一个漂亮的波浪。让我们继续下一步。
多个波浪
让我们更新我们的着色器以包含多个波浪。第一步，我将创建一个可重用的 wave_alpha 函数，该函数接收波浪的位置和高度，并返回一个 alpha 值。
float wave_alpha(float Y, float height) {
// ...
}为了保持整洁，我将创建一个 wave_noise 函数，返回我们在上一节定义的堆叠的 simplex 波浪：
float wave_noise() {
float noise = 0.0;
noise += simplex_noise(...) * ...;
noise += simplex_noise(...) * ...;
// ...
return noise;
}我们将使用它在 wave_alpha 中计算波浪的位置以及像素到它的距离：
float wave_alpha(float Y, float wave_height) {
float wave_y = Y + wave_noise() * wave_height;
float dist = wave_y - gl_FragCoord.y;
}使用距离计算 alpha 值：
float wave_alpha(float Y, float wave_height) {
float wave_y = Y + wave_noise() * wave_height;
float dist = wave_y - gl_FragCoord.y;
float alpha = clamp(0.5 + dist, 0.0, 1.0);
return alpha;
}然后我们将使用 wave_alpha 函数为两个波浪计算 alpha 值，每个波浪都有其独立的位置和高度：
const float WAVE1_HEIGHT = 24.0;
const float WAVE2_HEIGHT = 32.0;
const float WAVE1_Y = 0.80 * CANVAS_HEIGHT;
const float WAVE2_Y = 0.35 * CANVAS_HEIGHT;
float wave1_alpha = wave_alpha(WAVE1_Y, WAVE1_HEIGHT);
float wave2_alpha = wave_alpha(WAVE2_Y, WAVE2_HEIGHT);两个波浪将画布分为三部分。我喜欢将上部三分之一视为背景，并在其前面绘制两个波浪（波浪 1 位于中间，波浪 2 位于最前方）。
为了绘制背景和两个波浪，我们需要三种颜色。我选择了这些漂亮的蓝色：
vec3 background_color = vec3(0.102, 0.208, 0.761);
vec3 wave1_color = vec3(0.094, 0.502, 0.910);
vec3 wave2_color = vec3(0.384, 0.827, 0.898);最后，我们将通过使用两个波浪的 alpha 值混合这些颜色来计算像素的颜色：
vec3 color = background_color;
color = mix(color, wave1_color, wave1_alpha);
color = mix(color, wave2_color, wave2_alpha);
gl_FragColor = vec4(color, 1.0);这给我们以下结果：
我们确实得到了两个波浪，但它们完全同步。
这是有道理的，因为我们的噪声函数的输入是像素的位置和当前时间，这两个波浪都是相同的。
为了解决这个问题，我们将引入特定于波浪的偏移值，并将这些值传递给噪声函数。一种实现方法是直接为每个波浪提供一个字面值 offset ，并将其传递给噪声函数：
float wave_alpha(float Y, float wave_height, float offset) {
wave_noise(offset);
// ...
}
float w1_alpha = wave_alpha(WAVE1_Y, WAVE1_HEIGHT, -72.2);
float w2_alpha = wave_alpha(WAVE2_Y, WAVE2_HEIGHT, 163.9);然后 wave_noise 函数可以添加 offset 到 u_time 并在计算噪声时使用这个值。
float wave_noise(float offset) {
float time = u_time + offset;
float noise = 0.0;
noise += simplex_noise(x * L + F * time, time * S) * A;
// ...
}这会产生相同的波浪，但在时间上有所偏移。通过使偏移足够大，我们得到在时间上间隔足够远的波浪，以至于没有人会注意到它们实际上是同一个波浪。
但实际上我们不需要手动提供偏移。我们可以在 wave_alpha 函数中使用 Y 和 wave_height 参数推导出偏移值：
float wave_alpha(float Y, float wave_height) {
float offset = Y * wave_height;
wave_noise(offset);
// ...
}根据上述波常数和画布高度，我们得到以下偏移量：
有了这些偏移量，波浪在时间上相差秒。没人会注意到这一点。
加上偏移量后，我们得到两个不同的波浪：
现在我们已经更新了着色器来处理多个波浪，接下来让我们让波浪不再是单一的颜色。
动态 2D 噪声
在生成上述动画波浪时，我们使用 2D 噪声函数来生成动态 1D 噪声。
这种模式同样适用于更高维度。在生成 n 维噪声时，我们使用 n 维噪声函数，并将时间作为最后一个维度的值。
这是我们之前看到的静态 2D 单纯形噪声：
要实现动画效果，我们将使用 3D 单形噪声函数，将像素位置和坐标作为前两个参数，时间作为第三个参数。
const float L = 0.02;
const float S = 0.6;
float x = gl_FragCoord.x;
float y = gl_FragCoord.y;
float noise = simplex_noise(x * L, y * L, u_time * S);我们将对噪声进行归一化处理，并将其用作亮度值：
float lightness = (noise + 1.0) / 2.0;
gl_FragColor = vec4(vec3(lightness), 1.0);这样就得到了动态的 2D 噪声：
为了让噪点看起来像那样，我们需要做一些调整。让我们放大噪点，并且让噪点在轴上的比例比轴本身更大。
const float L = 0.0017;
const float S = 0.2;
const float Y_SCALE = 3.0;
float x = gl_FragCoord.x;
float y = gl_FragCoord.y * Y_SCALE;我将时间缩小了大约，并引入 Y_SCALE 使噪点在轴上更短。我还将速度降低了大约 80%。
通过这些调整，我们得到了以下噪点：
看起来相当不错，但噪点感觉分布得太均匀了。我们再次使用堆叠来让噪点更有趣。这是我想到的效果：
const float L = 0.0015;
const float S = 0.13;
const float Y_SCALE = 3.0;
float x = gl_FragCoord.x;
float y = gl_FragCoord.y * Y_SCALE;
float noise = 0.5;
noise += simplex_noise(x * L * 1.0, y * L * 1.00, u_time * S) * 0.30;
noise += simplex_noise(x * L * 0.6, y * L * 0.85, u_time * S) * 0.26;
noise += simplex_noise(x * L * 0.4, y * L * 0.70, u_time * S) * 0.22;
float lightness = clamp(noise, 0.0, 1.0);更大的噪声提供了更宽泛的渐变效果，而较小的噪声则赋予我们更精细的细节：
最后，我想再添加一个方向流动的组件。我会让其中两个噪声向左漂移，另一个向右漂移。
float F = 0.11 * u_time;
float sum = 0.5;
sum += simplex_noise(x ... + F * 1.0, ..., ...) * ...;
sum += simplex_noise(x ... + -F * 0.6, ..., ...) * ...;
sum += simplex_noise(x ... + F * 0.8, ..., ...) * ...;
float lightness = clamp(sum, 0.0, 1.0);这就是它的效果：
这使得噪声看起来像是向左流动——但并非均匀流动。
我认为这看起来相当不错！让我们将其整理到一个 background_noise 函数中：
float background_noise() {
float noise = 0.5;
noise += simplex_noise(...);
noise += simplex_noise(...);
// ...
return clamp(noise, 0.0, 1.0);
}
float lightness = background_noise()
gl_FragColor = vec4(vec3(lightness), 1.0);现在让我们超越黑白，为混合添加一些色彩！
色彩映射
这个红到蓝的渐变是通过根据像素的坐标计算一个值，并将其映射到一种红色和蓝色的混合色来实现的：
vec3 red = vec3(1.0, 0.0, 0.0);
vec3 blue = vec3(0.0, 0.0, 1.0);
float t = gl_FragCoord.x / (CANVAS_WIDTH - 1.0);
vec3 color = mix(red, blue, t);我们能做的是使用我们新的 background_noise 函数来计算这个值。
float t = background_noise();
vec3 color = mix(red, blue, t);这会起到将噪声映射到红到蓝渐变的效果：
这很酷，但我希望能将这个值映射到任何渐变上，比如这个：
这个渐变是一个 <div> 元素，其背景设置为这个 CSS 渐变：
background: linear-gradient(
90deg,
rgb(8, 0, 143) 0%,
rgb(250, 0, 32) 50%,
rgb(255, 204, 43) 100%
);我们可以在着色器中复制这个效果。首先，我们将渐变的三个颜色转换为 vec3 颜色：
vec3 color1 = vec3(0.031, 0.0, 0.561);
vec3 color2 = vec3(0.980, 0.0, 0.125);
vec3 color3 = vec3(1.0, 0.8, 0.169);然后我们使用一些巧妙的数学方法混合这些颜色：
float t = gl_FragCoord.x / (CANVAS_WIDTH - 1.0);
vec3 color = color1;
color = mix(color, color2, min(1.0, t * 2.0));
color = mix(color, color3, max(0.0, (t - 0.5) * 2.0));
gl_FragColor = vec4(color, 1.0);这完美地复制了 CSS 渐变：
我将颜色计算移入一个 calc_color 函数中，以使代码更清晰：
vec3 calc_color(float t) {
vec3 color = color1;
color = mix(color, color2, min(1.0, t * 2.0));
color = mix(color, color3, max(0.0, (t - 0.5) * 2.0));
return color;
}现在我们有了将值映射到渐变的 calc_color 函数，可以轻松地将 background_noise 映射到它：
float t = background_noise();
gl_FragColor = vec4(calc_color(t), 1.0);这是结果：
我们的 calc_color 函数已设置为处理 3 步渐变，但我们可以更新它以处理带步骤的渐变。这里是一个 5 步渐变的示例：
vec3 calc_color(float t) {
vec3 color1 = vec3(1.0, 0.0, 0.0);
vec3 color2 = vec3(1.0, 1.0, 0.0);
vec3 color3 = vec3(0.0, 1.0, 0.0);
vec3 color4 = vec3(0.0, 0.0, 1.0);
vec3 color5 = vec3(1.0, 0.0, 1.0);
float num_stops = 5.0;
float N = num_stops - 1.0;
vec3 color = mix(color1, color2, min(t * N, 1.0));
color = mix(color, color3, clamp((t - 1.0 / N) * N, 0.0, 1.0));
color = mix(color, color4, clamp((t - 2.0 / N) * N, 0.0, 1.0));
color = mix(color, color5, clamp((t - 3.0 / N) * N, 0.0, 1.0));
return color;
}上述函数产生以下效果：
这种方式可行，但像这样在代码中定义渐变（显然）并不理想。渐变颜色硬编码在我们的着色器中，我们需要手动调整函数以处理正确的颜色节点数量。
我们可以通过从纹理中读取渐变使其更动态。
渐变纹理
要将图像数据——例如线性渐变——从 JavaScript 传递到我们的着色器，我们可以使用纹理。纹理是数据数组，可以用来存储 2D 图像等。
首先，我们将在 JavaScript 中生成一个包含线性渐变的图像。我们将该图像写入一个纹理，并将该纹理传递给我们的 WebGL 着色器。然后着色器可以从纹理中读取数据。
将渐变渲染到画布上
我使用这个渐变生成器选择了以下渐变：
它由这些颜色组成：
const colors = [
"hsl(204deg 100% 22%)",
"hsl(199deg 100% 29%)",
"hsl(189deg 100% 32%)",
"hsl(173deg 100% 33%)",
"hsl(154deg 100% 39%)",
"hsl( 89deg 70% 56%)",
"hsl( 55deg 100% 50%)",
];要将渐变渲染到画布上，我们首先需要创建一个画布。我们可以这样做：
const canvas = document.createElement("canvas");
canvas.height = 256;
canvas.width = 64;
const ctx = canvas.getContext("2d");渐变像这样写入 CanvasGradient ：
const linearGradient = ctx.createLinearGradient(
0, 0, // Top-left corner
canvas.width, 0 // Top-right corner
);
for (const [i, color] of colors.entries()) {
const stop = i / (colors.length - 1);
linearGradient.addColorStop(stop, color);
}将渐变设置为活动填充样式，并在指定尺寸上绘制一个矩形，即可渲染渐变。
ctx.fillStyle = linearGradient;
ctx.fillRect(0, 0, canvas.width, canvas.height);
现在我们已经将线性渐变渲染到画布元素上，让我们将其写入纹理并传递给我们的着色器。
从着色器中读取画布内容
以下代码创建了一个 WebGL 纹理并将画布内容写入其中：
const texture = gl.createTexture();
gl.bindTexture(gl.TEXTURE_2D, texture);
gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, gl.RGBA, gl.UNSIGNED_BYTE, canvas);
gl.bindTexture(gl.TEXTURE_2D, null);我不会解释这段代码的工作原理——我想专注于着色器，而不是 WebGL API。如果你想更详细地了解如何将内容渲染到纹理上，我可以推荐你阅读这篇关于渲染到纹理的文章。
GLSL 着色器通过采样器从纹理中读取数据。采样器是一个函数，它接受纹理坐标并返回该位置纹理的值。强调“一个”值，因为当纹理坐标落在数据点之间时，采样器会返回一个插值结果，该结果由周围值推导而来。
对于不同的值类型有不同的采样器类型： isampler 用于有符号整数， usampler 用于无符号整数， sampler 用于浮点数。我们的图像纹理包含浮点数，所以我们将使用无前缀的 sampler 。
采样器还具有维度。你可以有 1D、2D 或 3D 采样器。由于我们将从 2D 图像纹理中读取数据，我们将使用 sampler2D 。如果你从 3D 纹理中读取无符号整数，你将使用 usampler3D 。
在我们的着色器中，我们将通过统一变量声明我们的采样器。我将将其命名为 u_gradient 。
uniform sampler2D u_gradient;在 JavaScript 方面，我们将 u_gradient 指向我们的 texture ，如下所示：
const gradientUniformLocation = gl.getUniformLocation(program, "u_gradient");
gl.activeTexture(gl.TEXTURE0);
gl.bindTexture(gl.TEXTURE_2D, texture);
gl.uniform1i(gradientUniformLocation, 0);同样，我不会解释这是如何工作的——我想专注于着色器方面——但我将您参考这篇关于 WebGL 纹理的文章。
要从纹理中读取数据（通过 sampler），我们将使用 OpenGL 的内置纹理查找函数之一。在我们的情况下，我们正在读取 2D 图像数据，因此我们将使用 texture2D 。
texture2D 接受两个参数，一个 sampler 和 2D 纹理坐标。坐标是标准化的，所以是纹理的左上角，是纹理的右下角。
注意： texture2D 坐标通常是归一化的，但采样器也可以使用“纹理空间”坐标，这些坐标的范围从...到...，其中...是该维度纹理的大小。
以下是参考用的我们的纹理：
该纹理在轴上是均匀的，因此我们可以直接设置坐标为（我们也可以使用或，结果会相同）。
由于该纹理在轴上是均匀的，所以它的高度无关紧要。我使用的高度为，因为在这个帖子中看起来不错，但你也可以使用高度为。
至于轴，在处读取颜色应该得到蓝色，在处我们应该得到黄色。我们可以用以下着色器来验证这一点
uniform sampler2D u_gradient;
uniform float u_x;
void main() {
gl_FragColor = texture2D(u_gradient, vec2(u_x, 0.5));
}在下面的画布中，滑块控制 u_x 的值。当你从滑动到时，颜色应该从蓝色变为黄色：
它起作用了！现在我们可以将值映射到渐变纹理之间。这使得将 background_noise 映射到渐变变得很简单：
uniform sampler2D u_gradient;
float t = background_noise();
gl_FragColor = texture2D(u_gradient, vec2(t, 0.5));正如我们所见，这的效果是将我们的渐变应用于背景噪声：
在 JavaScript 中定义渐变并动态生成它给了我们很大的灵活性。我们可以轻松地改变渐变，比如，变成这个酷炫的粉彩色渐变：
const colors = [
"hsl(141 75% 72%)",
"hsl(41 90% 62%)",
"hsl(358 64% 50%)",
];
我们很快会在最终效果中使用这个，但在我们到达那里之前，让我们完成波浪的混合。
动态模糊
在最终效果中，我们看到每个波浪都应用了不同程度的模糊，模糊程度会随时间变化。
然而，我们当前的波浪边缘很锐利。
让我们开始构建动态模糊效果。简单回顾一下，我们目前计算波浪透明度的方式如下：
float x = gl_FragCoord.x;
float y = gl_FragCoord.y;
float wave_alpha(float Y, float wave_height) {
float offset = Y * wave_height;
float wave_y = Y + wave_noise(offset) * wave_height;
float dist = wave_y - y;
float alpha = clamp(0.5 + dist, 0.0, 1.0);
return alpha;
}让我们定义一个函数来计算应应用的模糊量。我们先用一个从左到右逐渐增加的模糊效果作为起点，覆盖整个画布宽度：
float calc_blur() {
float t = x / (CANVAS_WIDTH - 1.0);
float blur = mix(1.0, BLUR_AMOUNT, t);
return blur;
}我们将用它来计算一个 blur 值，并将 dist 除以它——就像我们在这篇文章前面所做的那样：
float blur = calc_blur();
float alpha = clamp(0.5 + dist / blur, 0.0, 1.0);这给我们带来了从左到右的模糊效果：
为了让模糊效果变得动态，我们再次使用简单的噪声函数。设置应该感觉很熟悉，它几乎与我们之前定义的 wave_noise 函数相同：
float calc_blur() {
const float L = 0.0018;
const float S = 0.1;
const float F = 0.034;
float noise = simplex_noise(x * L + F * u_time, u_time * S);
float t = (noise + 1.0) / 2.0;
float blur = mix(1.0, BLUR_AMOUNT, t);
return blur;
}如果我们直接将这个应用到我们的波浪上，每个波浪的模糊效果看起来都会相同。为了让波浪的模糊效果不同，我们需要为 u_time 添加一个偏移量。
方便的是，我们可以复用为 wave_noise 函数计算过的相同偏移量：
float calc_blur(float offset) {
float time = u_time * offset;
float noise = simplex_noise(x * L + F * time, time * S);
// ...
}
float wave_alpha(float Y, float wave_height) {
float offset = Y * wave_height;
float wave_y = Y + wave_noise(offset) * wave_height;
float blur = calc_blur(offset);
// ...
}这给我们带来了动态模糊效果：
但说实话，模糊效果看起来相当糟糕。感觉每个波浪的顶部和底部都有明显的“边缘”。
此外，波浪整体感觉有些模糊，只是分布不均匀。
让我们先修复生硬的边缘。
让模糊效果更好
考虑我们是如何计算 alpha 的：
float alpha = clamp(0.5 + dist / blur, 0.0, 1.0);当距离等于α时，它就等于α。然后它线性增加或减少，直到达到 0 或 1，此时 clamp 函数开始起作用。
让我们绘制α曲线，以便我们能够直观地看到这一点：
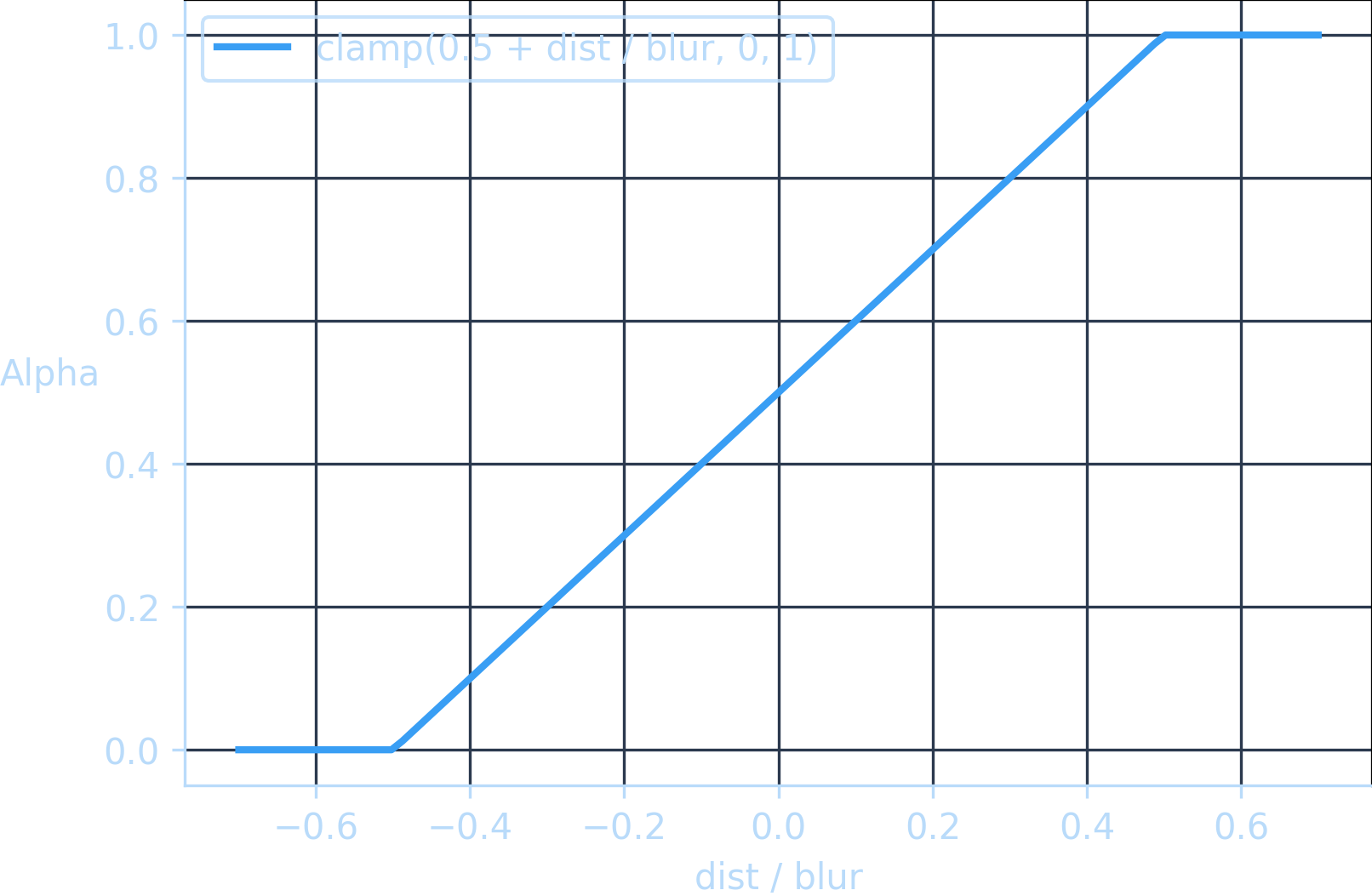
在模糊边缘处，0 和 1 的突然变化产生了我们观察到的锐利边缘。
smoothstep 函数可以在这里派上用场。smoothstep 是一系列插值函数，正如其名，它们平滑地过渡从到。
我将 smoothstep 定义如下：
float smoothstep(float t) {
return t * t * t * (t * (6.0 * t - 15.0) + 10.0);
}这是平滑步进函数的“五次方”变体。它比“默认”的平滑步进实现提供了更多的平滑效果。
将 smoothstep 应用于我们的 alpha 曲线非常简单：
float alpha = clamp(0.5 + dist / blur, 0.0, 1.0);
alpha = smoothstep(alpha);下面是一个显示平滑 alpha 曲线的图表——我将包含原始未平滑的曲线以供比较：
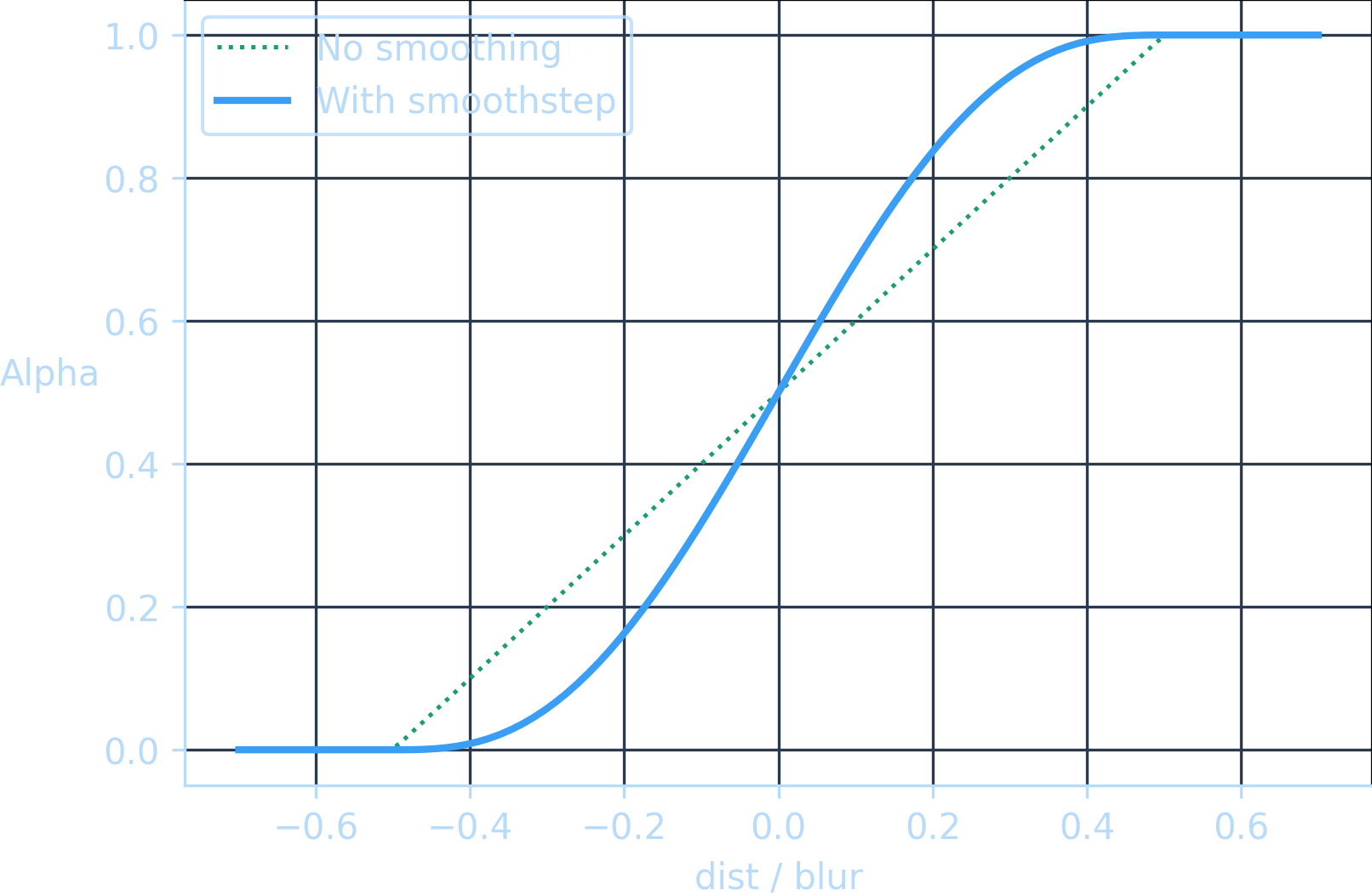
这产生了一个更平滑的模糊效果：
以下是并排比较。左侧的模糊效果被平滑处理，而右侧的则没有。
那解决了锐利的边缘问题。现在我们来处理波浪整体过于模糊的问题。
让波浪不那么均匀地模糊
这是我们留下的 calc_blur 方法：
float calc_blur() {
// ...
float noise = simplex_noise(x * L + F * u_time, u_time * S);
float t = (noise + 1.0) / 2.0;
float blur = mix(1.0, BLUR_AMOUNT, t);
return blur;
}当接近时，边缘变得更锐利，当接近时，边缘变得更模糊。然而，波浪只有在非常接近零时才会变得锐利。
下面的画布有一个可视化图表来说明这一点。下半部分是一个图表，显示了轴上的值（从底部到顶部）：
你会注意到，当图表接近底部时——即值接近零时——波浪会变得尖锐，但它很少会那么低。l 的值在中途徘徊太多，导致整个波浪看起来有些模糊。
我们可以通过将 l 的值提高到某个幂——即应用指数——来使 l 的值接近 l。
考虑指数如何影响和之间的值。接近的数会受到向的强烈吸引，而较大的数受到的吸引较小。例如，会减少 90%，而只会减少 10%。
拉力的大小取决于指数。以下是介于 a 和 b 之间的不同 a 值对应的图表：
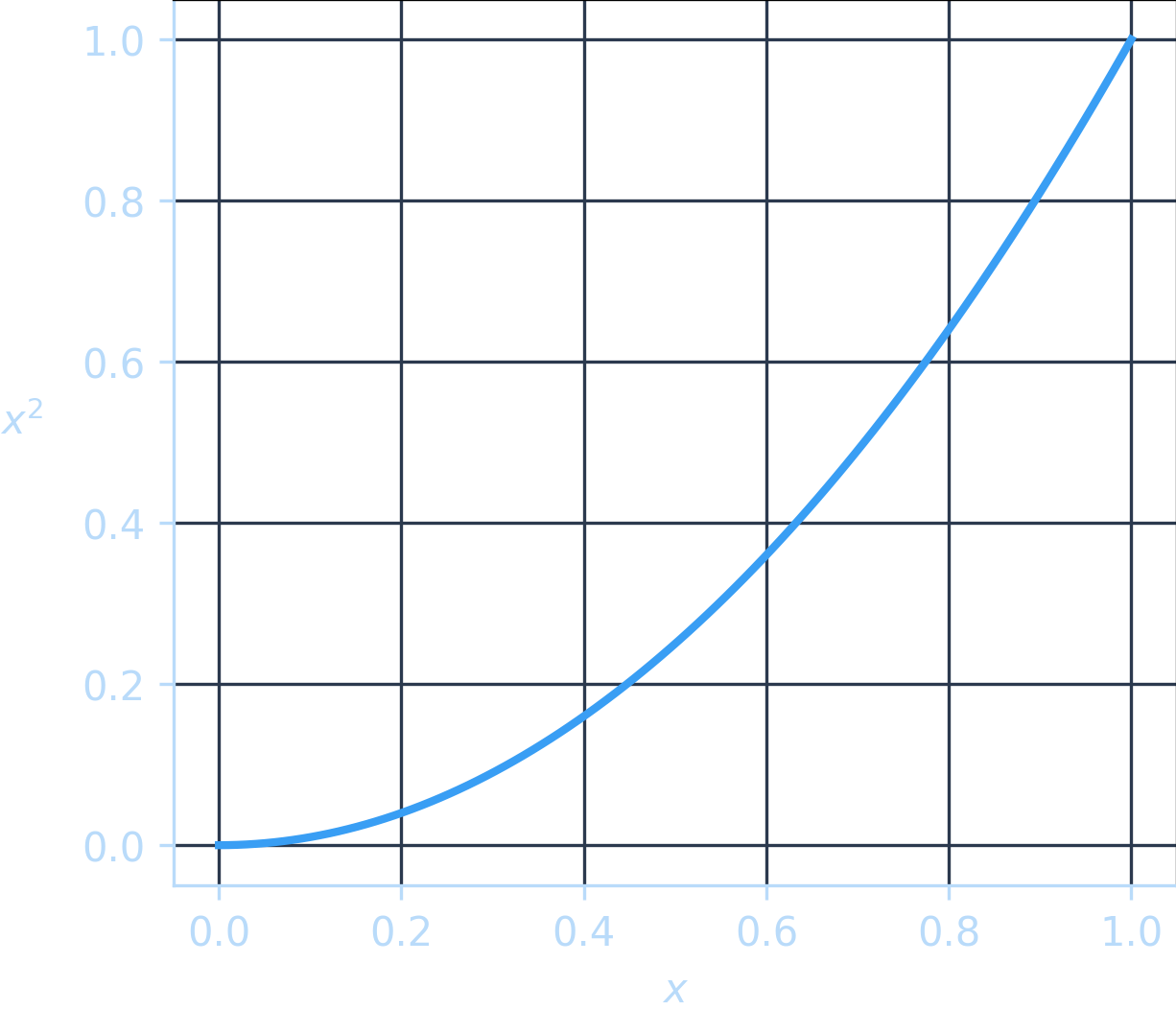
随着指数的增加，这种效果会更加明显：
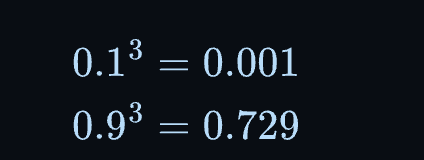
a 变小了，而 b 大致变小了！
下面的图表展示了不同 a 值在 a 到 b 范围内的变化情况：
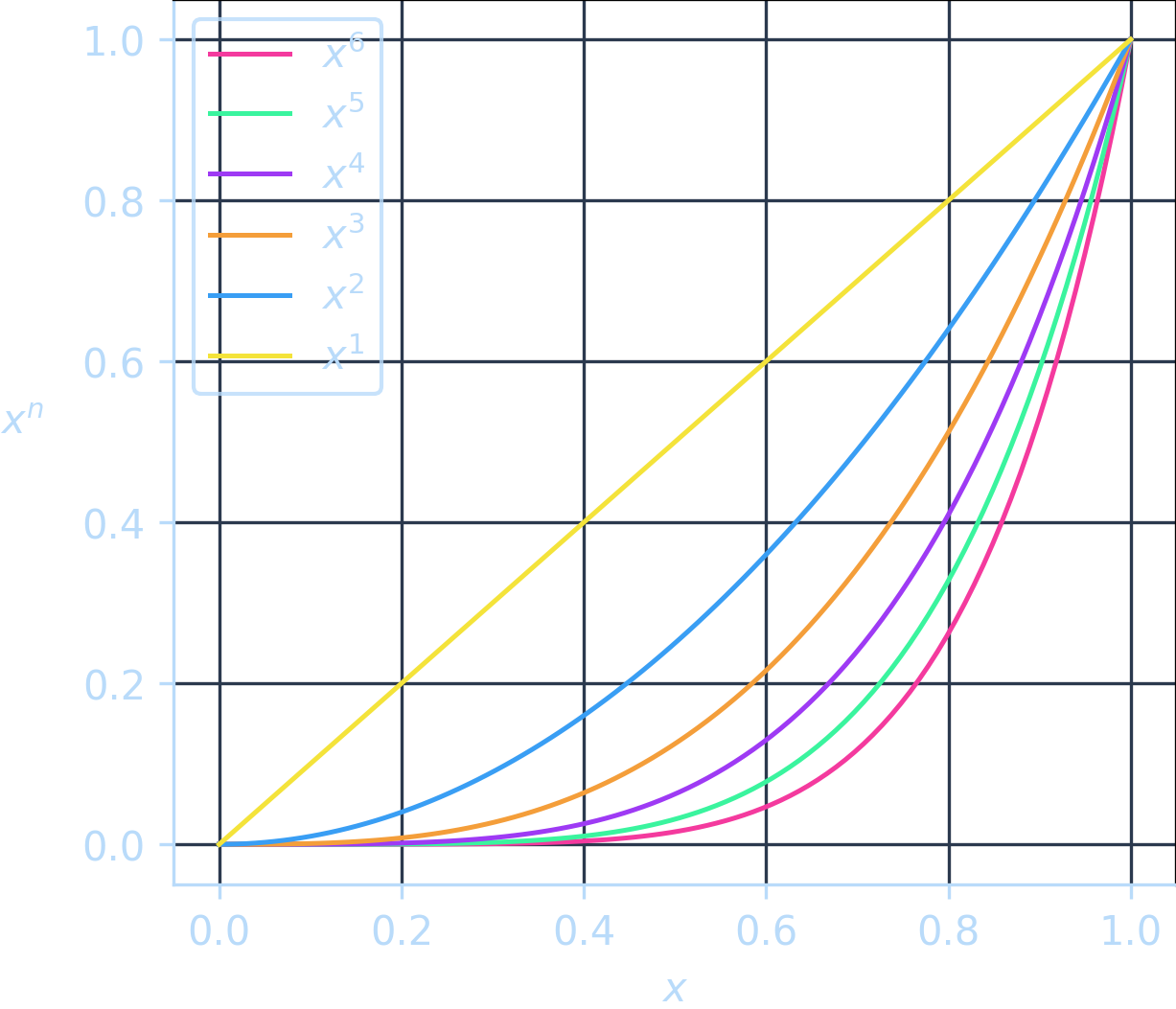
注意到指数为 0 时没有效果。
如您所见，指数越高，向零的拉力就越强。
那么，让我们对 x 应用一个指数。我们可以使用内置的 pow 函数来实现：
float t = (noise + 1.0) / 2.0;
t = pow(t, exponent);下面是一个画布，允许你调整 exponent 的值从 0 到 1。我故意将 exponent 设置为默认值 0（无效果），这样你就能直接看到增加指数的效果（留下的浅蓝色线表示应用指数前的值）。
随着指数的增加，它会越来越“贴近”图表的底部。这会产生明显的相对锐利时期，同时不会过度压制较高值。我觉得指数为 2 会得到不错的结果——我选择 2。
让我们把另一个波形带回来，看看我们得到了什么：
应用指数确实会减弱模糊的强度，所以让我们增加模糊量——我将它从 1 增加到 2。
.
现在我们谈正事了！我们得到了一个非常漂亮的模糊效果！
将所有内容整合在一起
我们已经拥有了构建最终效果所需的所有独立部件——让我们最终将它们整合在一起！
每个波浪都由一个 alpha 值表示：
float w1_alpha = wave_alpha(WAVE1_Y, WAVE1_HEIGHT);
float w2_alpha = wave_alpha(WAVE2_Y, WAVE2_HEIGHT);我们目前正使用这些 alpha 值来混合三种颜色——这些来自上一节的蓝色调：
vec3 bg_color = vec3(0.102, 0.208, 0.761);
vec3 wave1_color = vec3(0.094, 0.502, 0.910);
vec3 wave2_color = vec3(0.384, 0.827, 0.898);我们最终效果的关键在于用独特的背景噪声替换每种颜色，并将它们混合在一起。
我们需要让这三个背景噪声保持独特。为了支持这一点，我们将更新我们的 background_noise 函数以接受一个偏移值并将其添加到 u_time 。我们之前已经做过两次，所以在这个阶段这只是一个常规操作：
float background_noise(float offset) {
float time = u_time + offset;
float noise = 0.5;
noise += simplex_noise(..., time * S) * ...;
noise += simplex_noise(..., time * S) * ...;
// ...
return clamp(noise, 0.0, 1.0);
}现在我们可以轻松生成多个独特的背景噪声。让我们从将背景噪声解释为亮度值开始：
float bg_lightness = background_noise(0.0);
float w1_lightness = background_noise(200.0);
float w2_lightness = background_noise(400.0);我们可以使用波浪形 alpha 值来混合这些亮度值，以计算最终的 lightness 值，并将 vec3(lightness) 传递给 gl_FragColor ：
float lightness = bg_lightness;
lightness = mix(lightness, w1_lightness, w1_alpha);
lightness = mix(lightness, w2_lightness, w2_alpha);
gl_FragColor = vec4(vec3(lightness), 1.0);这给我们带来了以下效果：
试着告诉我这个效果不绝对酷炫！它流畅、流动，有时还相当戏剧化。
下一步很显然是将最终的 lightness 值映射到渐变上。我们使用这个：
和之前一样，我们将纹理通过 uniformsampler2D 输入到我们的着色器中：
uniform sampler2D u_gradient;我们接着将亮度值映射到渐变上，如下所示：
gl_FragColor = texture2D(u_gradient, vec2(lightness, 0.5));这将渐变应用到我们的效果上：
结语
我希望这能是一个很好的着色器编写入门介绍，并且希望我为你提供了开始自己编写着色器的工具和直觉！
原文地址
https://alexharri.com/blog/webgl-gradients?utm_source=chatgpt.com (opens in a new tab)